10701. Прямой, центрированный и обратный порядок
Классическими методами обхода
деревьев являются:
·
прямой: посещается корень, левое поддерево, правое поддерево;
·
центрированный: посещается левое поддерево, корень, правое поддерево;
·
обратный: посещается левое поддерево, правое поддерево, корень;
Рассмотрим рисунок:
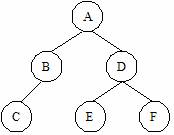
Прямой, центрированный и обратный
обходы соответственно дадут следующие последовательности вершин: ABCDEF,
CBAEDF, CBEFDA. В задаче требуется найти последовательность вершин при обратном
обходе, если известны прямой и центрированный обходы.
Вход. Первая строка содержит
количество тестов C (C £ 2000). Каждая следующая строка является отдельным тестом и
содержит количество вершин в бинарном дереве n (1 £ n £ 52) и две строки S1 и
S2 , содержащие соответственно прямой и центрированный обход дерева.
Выход. Для каждого теста вывести
последовательность вершин при обратном обходе дерева.
Пример входа
3
3 xYz Yxz
3 abc cba
6 ABCDEF CBAEDF
Пример выхода
Yzx
Cba
CBEFDA
РЕШЕНИЕ
структуры данных, рекурсия
Анализ алгоритма
Корень дерева (обозначим его
через A) содержится в начале последовательности прямого обхода. Пусть
последовательность прямого обхода имеет вид Ax2x3…xn,
центрированного – y1y2…ykAyk+2…yn.
В центрированном обходе ищем корень A. Тогда левое поддерево содержит вершины y1y2…yk
(всего k вершин), а правое yk+2…yn.
Пример
Структура дерева для третьего теста приведена выше.
Реализация алгоритма
В символьных массивах pre_order и
in_order будем хранить последовательность вершин при прямом и центрированном
обходе дерева.
char pre_order[53],in_order[53];
Пусть последовательность вершин
при прямом обходе некоего поддерева содержится в ячейках от pre_order[prea] до
pre_order[preb], а при центрированном – в ячейках от in_order[ina] до
in_order[inb]. Тогда функция post_order напечатает это поддерево в обратном
порядке.
void post_order(int
ina, int inb, int
prea,int preb)
{
int
lsize,rt_in;
char root;
if (ina ==
inb) return;
root = pre_order[prea];
for(rt_in = ina;
rt_in < inb; rt_in++)
if
(in_order[rt_in] == root) break;
lsize = rt_in - ina;
post_order(ina,rt_in,prea+1,prea+lsize);
post_order(rt_in+1,inb,prea+1+lsize,preb);
printf("%c",root);
}
Читаем число тестов n. Для
каждого теста читаем количество вершин дерева d и последовательность
вершин при прямом и центрированном обходе дерева. Запускаем процедуру
post_order, которая и выводит искомый обратный порядок вершин.
scanf("%d",&n);
for(i = 0; i < n; i++)
{
scanf("%d %s
%s",&d,pre_order,in_order);
post_order(0,strlen(pre_order),0,strlen(in_order));
printf("\n");
}